Recently there have been surprising discussions and disputes amongst philosophers and physicists about an elementary probability problem called the Sleeping Beauty problem. The following remarks are, as usual in this blog, the result of discussions with Nicoletta Sabadini.
The problem goes as follows: A beauty is told that the following procedure will be carried out. On Sunday a fair coin will be tossed without her knowing the result. She will go to sleep. Then on Monday one of two possibilities will occur.
In the case that the toss of the coin resulted in tails she will be wakened and asked her opinion of the probability that the result of coin was heads. She will then have her memory of what happened on Monday erased and will be put to sleep. On Tuesday (again in the case of tails, without a further toss of the coin) she will be wakened and asked her estimate of the result of the coin toss being heads.
In the case of heads, on Monday she will be asked her estimate of the probability that the result of the coin toss was heads. In that case she will not be asked again.
It seems clear intuitively that, when this procedure is carried out, in all three responses she has learnt nothing about the result of the coin toss, and that she should answer in each case $1/2$.
Strangely a considerable number of philosophers and physicists make an elementary error in the calculation of probabilities and believe that she should answer $1/3$.
The philosophers who come to this conclusion include professors at Princeton and Oxford. The physicists include a Senior Research Associate at Caltech, who manages to involve quantum mechanics and the multiverse. (Not all physicists agree - for example, the maverick (or main stream?) physicist Lubos Motl is scathing about the answer $1/3$.)
Let's see how they manage to come to the $1/3$ conclusion and what their elementary error is.
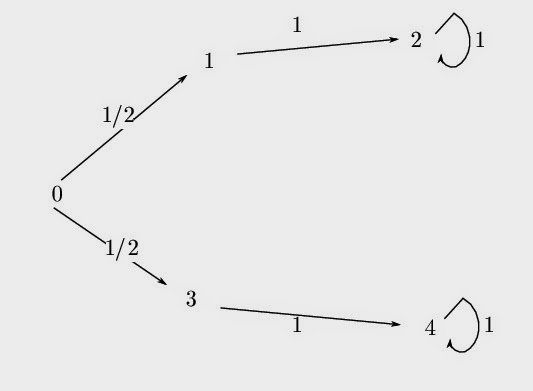
We can describe the procedure by a simple Markov chain, pictured below, in which the initial state (Sunday) is $0$, the state $1$ is Monday in the case of heads, the state $2$ is Tuesday and subsequent dates after heads, the state $3$ is Monday in the case of tails, the state $4$ is Tuesday and subsequent dates in the case tails.
Now the argument of the philosophers/physicists mentioned above is that when the beauty is awakened she knows she is in one of states 1, 3 or 4 but she doesn't know which.
They claim that being in each of these three states has the same probability, and hence this probability must be $1/3$ (the sum must be $1$). But in state $1$ she knows the coin was heads, and in $3$ and $4$ the coin was tails. So in a third of cases the coin is heads, so she must answer $1/3$.
The egregious error!
In a Markov process one cannot in general talk about the probability of being in a state. One must talk about the probabilityof passing from state $x$ to state $y$ in $n$ steps.
(If the process is ergodic then in a limiting distribution there is some sense of talking about the probability of being in a state, but that is not the case here.)
The three probabilities discussed above are (i) the probability $p_1$ of going from $0$ to $1$ in one step, (ii) the probability $p_3$ of going from $0$ to $3$ in one step, and (iii) the probability $p_4$ of going from $0$ to $4$ in two steps. Each of these three values is clearly $1/2$.
What however should the beauty calculate for the probability $p_{3,4}$ of being either in $3$ in one step or $4$ in two steps? The philosophers/physicists are claiming that $p_{3,4}=2p_1$. I claim $p_{3,4}=p_1$. To see this we need to think in general how to calculate the probability of going from state $x$ to $y$ in $m$ or $n$ steps in a Markov chain.
Take $x$ to be a fixed initial state, which we wont mention again. The sum over all $y$ of $p_{one}(y)$ (the probability of reaching $y$ in one step) is $1$. The sum over all $y$ of $p_{two}(y)$ (the probability of reaching $y$ in two steps) is $1$. Hence taking $p_{one,two}(y)=p_{one}(y)+p_{two}(y)$ as the physicists/philosophers do would yield $\sum_yp_{one,two}(y)=2$ whereas the total probability should be one.
A reasonable definition for $p_{one,two}$ would be $p_{one,two}(y)=\frac{1}{2}( p_{one}(y)+p_{two}(y))$.
This definition yields in the sleeping beauty problem that $p_{3,4}=\frac{1}{2}(p_3+p_4)= \frac{1}{2}=p_1$.
The problem goes as follows: A beauty is told that the following procedure will be carried out. On Sunday a fair coin will be tossed without her knowing the result. She will go to sleep. Then on Monday one of two possibilities will occur.
In the case that the toss of the coin resulted in tails she will be wakened and asked her opinion of the probability that the result of coin was heads. She will then have her memory of what happened on Monday erased and will be put to sleep. On Tuesday (again in the case of tails, without a further toss of the coin) she will be wakened and asked her estimate of the result of the coin toss being heads.
In the case of heads, on Monday she will be asked her estimate of the probability that the result of the coin toss was heads. In that case she will not be asked again.
It seems clear intuitively that, when this procedure is carried out, in all three responses she has learnt nothing about the result of the coin toss, and that she should answer in each case $1/2$.
Strangely a considerable number of philosophers and physicists make an elementary error in the calculation of probabilities and believe that she should answer $1/3$.
The philosophers who come to this conclusion include professors at Princeton and Oxford. The physicists include a Senior Research Associate at Caltech, who manages to involve quantum mechanics and the multiverse. (Not all physicists agree - for example, the maverick (or main stream?) physicist Lubos Motl is scathing about the answer $1/3$.)
Let's see how they manage to come to the $1/3$ conclusion and what their elementary error is.
We can describe the procedure by a simple Markov chain, pictured below, in which the initial state (Sunday) is $0$, the state $1$ is Monday in the case of heads, the state $2$ is Tuesday and subsequent dates after heads, the state $3$ is Monday in the case of tails, the state $4$ is Tuesday and subsequent dates in the case tails.
Now the argument of the philosophers/physicists mentioned above is that when the beauty is awakened she knows she is in one of states 1, 3 or 4 but she doesn't know which.
They claim that being in each of these three states has the same probability, and hence this probability must be $1/3$ (the sum must be $1$). But in state $1$ she knows the coin was heads, and in $3$ and $4$ the coin was tails. So in a third of cases the coin is heads, so she must answer $1/3$.
The egregious error!
In a Markov process one cannot in general talk about the probability of being in a state. One must talk about the probabilityof passing from state $x$ to state $y$ in $n$ steps.
(If the process is ergodic then in a limiting distribution there is some sense of talking about the probability of being in a state, but that is not the case here.)
The three probabilities discussed above are (i) the probability $p_1$ of going from $0$ to $1$ in one step, (ii) the probability $p_3$ of going from $0$ to $3$ in one step, and (iii) the probability $p_4$ of going from $0$ to $4$ in two steps. Each of these three values is clearly $1/2$.
What however should the beauty calculate for the probability $p_{3,4}$ of being either in $3$ in one step or $4$ in two steps? The philosophers/physicists are claiming that $p_{3,4}=2p_1$. I claim $p_{3,4}=p_1$. To see this we need to think in general how to calculate the probability of going from state $x$ to $y$ in $m$ or $n$ steps in a Markov chain.
Take $x$ to be a fixed initial state, which we wont mention again. The sum over all $y$ of $p_{one}(y)$ (the probability of reaching $y$ in one step) is $1$. The sum over all $y$ of $p_{two}(y)$ (the probability of reaching $y$ in two steps) is $1$. Hence taking $p_{one,two}(y)=p_{one}(y)+p_{two}(y)$ as the physicists/philosophers do would yield $\sum_yp_{one,two}(y)=2$ whereas the total probability should be one.
A reasonable definition for $p_{one,two}$ would be $p_{one,two}(y)=\frac{1}{2}( p_{one}(y)+p_{two}(y))$.
This definition yields in the sleeping beauty problem that $p_{3,4}=\frac{1}{2}(p_3+p_4)= \frac{1}{2}=p_1$.